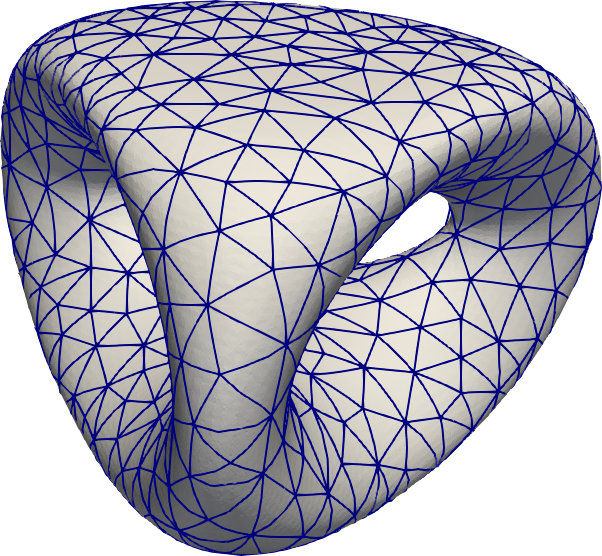
Dune-CurvedGrid - A Dune module for surface parametrization
Identifiers (Article)
Abstract
In this paper we introduce and describe an implementation of curved (surface) geometries within the Dune framework for grid-based discretizations. Therefore, we employ the abstraction of geometries as local-functions bound to a grid element, and the abstraction of a grid as connectivity of elements together with a grid-function that can be localized to the elements to provide element local parametrizations of the curved surface.
Statistics
References
J. Ahrens, B. Geveci, and C. Law. ParaView: An End-User Tool for Large Data Visualization. Visualization Handbook. Elsevier, 2005. ISBN 978-0123875822.
R. Anderson, J. Andrej, A. Barker, J. Bramwell, J.-S. Camier, J. Cerveny, V. Dobrev, Y. Dudouit, A. Fisher, T. Kolev, W. Pazner, M. Stowell, V. Tomov, I. Akkerman, J. Dahm, D. Medina, and S. Zampini. MFEM: A modular finite element methods library. Computers & Mathematics with Applications, 81:42–74, jan 2021. doi: 10.1016/j.camwa.2020.06.009.
D. Arndt, W. Bangerth, D. Davydov, T. Heister, L. Heltai, M. Kronbichler, M. Maier, J.-P. Pelteret, B. Turcksin, and D. Wells. The deal.II finite element library: Design, features, and insights. Journal of Numerical Mathematics, 81:407–422, jan 2021. doi: 10.1016/j.camwa.2020.02.022. URL https://dealii.org.
P. Bastian, M. Blatt, A. Dedner, N.-A. Dreier, C. Engwer, R. Fritze, C. Gräser, D. Kempf, R. Klöfkorn, M. Ohlberger, and O. Sander. The dune framework: Basic concepts and recent developments. Computers & Mathematics with Applications, 81:75–112, 2021. ISSN 0898-1221. doi: 10.1016/j. camwa.2020.06.007.
J. L. Blanco and P. K. Rai. nanoflann: a C++ header-only fork of FLANN, a library for nearest neighbor (NN) with kd-trees, 2014. URL https://github.com/jlblancoc/nanoflann. D. Bothe and A. Reusken, editors. Transport Processes at Fluidic Interfaces. Springer International Publishing, 2017. doi: 10.1007/978-3-319-56602-3.
E. Burman, P. Hansbo, M. G. Larson, and A. Massing. Cut finite element methods for partial differential equations on embedded manifolds of arbitrary codimensions. ESAIM: Mathematical Modelling and Numerical Analysis, 52(6):2247–2282, 2018. doi: 10.1051/m2an/2018038.
K. Deckelnick, G. Dziuk, and C. M. Elliott. Computation of geometric partial differential equations and mean curvature flow. Acta Numerica, 14:139–232, 2005. doi: 10.1017/S0962492904000224.
A. Dedner and M. Nolte. Construction of local finite element spaces using the generic reference elements. In A. Dedner, B. Flemisch, and R. Klöfkorn, editors, Advances in DUNE, pages 3–16, Berlin, Heidelberg, 2012. Springer Berlin Heidelberg. ISBN 978-3-642-28589-9. doi: 10.1007/ 978-3-642-28589-9_1.
A. Demlow. Higher-order finite element methods and pointwise error estimates for elliptic problems on surfaces. SIAM Journal on Numerical Analysis, 47(2):805–827, 2009. doi: 10.1137/ 070708135.
A. Demlow and G. Dziuk. An adaptive finite element method for the Laplace–Beltrami operator on implicitly defined surfaces. SIAM Journal on Numerical Analysis, 45(1):421–442, 2007. doi: 10.1137/050642873.
G. Dziuk. An algorithm for evolutionary surfaces. Numerische Mathematik, 58:603–611, 1990. doi: 10.1007/BF01385643.
G. Dziuk and C. M. Elliott. Finite element methods for surface pdes. Acta Numerica, 22:289–396, 2013. doi: 10.1017/S0962492913000056.
C. Engwer and A. Nüßing. Geometric reconstruction of implicitly defined surfaces and domains with topological guarantees. ACM Transactions on Mathematical Software, 44(2), 2017. doi: 10.1145/3104989.
C. Engwer, C. Gräser, S. Müthing, and O. Sander. The interface for functions in the dune-functions module. Archive of Numerical Software, 5(1):95–110, 2017. doi: 10.11588/ans.2017.1.27683. C. Engwer, C. Gräser, S. Müthing, and O. Sander. Function space bases in the dune-functions module. arXiv, 2018, 1806.09545.
W. Freeden and M. Schreiner. Spherical Functions of Mathematical Geosciences. Springer Berlin Heidelberg, 2009. doi: 10.1007/978-3-540-85112-7.
H. Fritz. Isoparametric finite element approximation of Ricci curvature. IMA Journal of Numerical Analysis, 33(4):1265–1290, 2013. doi: 10.1093/imanum/drs037.
C. Geuzaine and J.-F. Remacle. Gmsh: A 3-d finite element mesh generator with built-in pre- and post-processing facilities. International Journal for Numerical Methods in Engineering, 79(11): 1309–1331, 2009. doi: 10.1002/nme.2579. URL https://gmsh.info.
J. Grande, C. Lehrenfeld, and A. Reusken. Analysis of a high-order trace finite element method for PDEs on level set surfaces. SIAM Journal on Numerical Analysis, 56(1):228–255, 2018. doi: 10.1137/16M1102203.
S. Gross, T. Jankuhn, M. A. Olshanskii, and A. Reusken. A trace finite element method for vector-Laplacians on surfaces. SIAM Journal on Numerical Analysis, 56(4):2406–2429, 2018. doi: 10.1137/17M1146038.
P. Hansbo, M. G. Larson, and K. Larsson. Analysis of finite element methods for vector Laplacians on surfaces. IMA Journal of Numerical Analysis, 04 2019. doi: 10.1093/imanum/drz018. H. Hardering and S. Praetorius. Tangential errors of tensor surface finite elements. arXiv, Jun 2021, 2106.01000. arxiv:2106.01000.
C. J. Heine. Isoparametric finite element approximation of curvature on hypersurfaces. Technical report, Abteilung für Angewandte Mathematik, Universität Freiburg, Hermann-Herder-Straße 10, 79104 Freiburg i.Br., Germany, 2004.
T. Jankuhn and A. Reusken. Trace finite element methods for surface vector-Laplace equations. 41(1):48–83, may 2020. doi: 10.1093/imanum/drz062.
T. Jankuhn, M. Olshanskii, and A. Reusken. Incompressible fluid problems on embedded surfaces: modeling and variational formulations. Interfaces and Free Boundaries, 20(3):353–377, 2018. doi: 10.4171/IFB/405.
A. Johnen, J.-F. Remacle, and C. Geuzaine. Geometrical validity of high-order triangular finite elements. Engineering with Computers, 30(3):375–382, 2014. doi: 10.1007/s00366-012-0305-7.
B. Kovács, B. Li, and C. Lubich. A convergent evolving finite element algorithm for mean curvature flow of closed surfaces. Numerische Mathematik, 143:797–853, 2019. doi: 10.1007/s00211-019-01074-2.
C. Lehrenfeld. High order unfitted finite element methods on level set domains using isoparametric mappings. Computer Methods in Applied Mechanics and Engineering, 300:716–733, 2016. doi: 10.1016/j.cma.2015.12.005.
M. Nestler, I. Nitschke, S. Praetorius, and A. Voigt. Orientational order on surfaces: The coupling of topology, geometry, and dynamics. Journal of Nonlinear Science, 28(1):147–191, 2017. doi: 10.1007/s00332-017-9405-2.
M. Nestler, I. Nitschke, and A. Voigt. A finite element approach for vector- and tensor-valued surface pdes. Journal of Computational Physics, 389:48–61, 2019. doi: 10.1016/j.jcp.2019.03.006.
I. Nitschke. Diskretes Äußeres Kalkül (DEC) auf Oberflächen ohne Rand. Master’s thesis, Technische Universität Dresden, Dresden, 2014.
M. A. Olshanskii and A. Reusken. Trace finite element methods for PDEs on surfaces. In Lecture Notes in Computational Science and Engineering, pages 211–258. Springer International Publishing, 2017. doi: 10.1007/978-3-319-71431-8_7.
P.-O. Persson. Mesh Generation for Implicit Geometries. PhD thesis, Department of Mathematics, MIT, Dec 2004.
P.-O. Persson and G. Strang. A simple mesh generator in MATLAB. SIAM Review, 46(2):329–345, 2004. doi: 10.1137/S0036144503429121.
S. Praetorius. Dune-Vtk – grid reader and writer for the vtk file format, 2019. URL https://gitlab.dune-project.org/extensions/dune-vtk.
S. Praetorius. Dune-CurvedGeometry – parametrizations of curved geometries, 2020. URL https://gitlab.mn.tu-dresden.de/iwr/dune-curvedgeometry.
S. Praetorius and F. Stenger. Dune-CurvedGrid – meta grid for wrapping element geometries into a curved geometries, 2020a. URL https://gitlab.mn.tu-dresden.de/iwr/dune-curvedgrid.
S. Praetorius and F. Stenger. Example codes of this manuscript collected in a dune module, 2020b. URL https://gitlab.mn.tu-dresden.de/iwr/dune-curvedgrid-examples.
S. Praetorius and F. Stenger. Dune-Gmsh4 – grid reader and writer for the gmsh-4 file format, 2020c. URL https://gitlab.mn.tu-dresden.de/iwr/dune-gmsh4.
A. Rätz and A. Voigt. PDE’s on surfaces — a diffuse interface approach. Communications in Mathematical Sciences, 4(3):575–590, 09 2006. URL https://projecteuclid.org:443/euclid.cms/1175797557.
O. Sander, T. Koch, N. Schröder, and B. Flemisch. The Dune-FoamGrid implementation for surface and network grids. Archive of Numerical Software, 5(1):217–244, 2017. doi: 10.11588/ans. 2017.1.28490.
J. Schöberl. NETGEN an advancing front 2d/3d-mesh generator based on abstract rules. Computing and Visualization in Science, 1(1):41–52, Jul 1997. doi: 10.1007/s007910050004.
J. Schöberl. C++11 implementation of finite elements in NGSolve. Technical report, Institute for analysis and scientific computing, Vienna University of Technology, 2014. URL https://ngsolve.org.
F. Stenger. meshconv: a tool for various mesh-conversions and mesh-transformations., 2020. URL https://gitlab.mn.tu-dresden.de/iwr/meshconv. v3.20.
S. Valette and J.-M. Chassery. Approximated centroidal Voronoi diagrams for uniform polygonal mesh coarsening. Computer Graphics Forum, 23(3):381–389, 2004. doi: 10.1111/j.1467-8659.2004. 00769.x.